pulsebible.blogg.se - Descriptive analysis in excel for mac

#Descriptive analysis in excel for mac how to
#Descriptive analysis in excel for mac software

We can use statistics related to the normal curve to calculate how we might expect bins to behave given the median and standard deviation of our sample. That information is housed in the data table Excel (Sheet 2) creates to make the histogram (refer blue histogram image above) The Expected Bins Having created a histogram via the Analysis ToolPak, you already have access to the observed bin distribution. In this case, it is the size of the p-Value that lets us decide whether to accept or reject the hypothesis that the data is normal.įor the purpose of the Chi-Squared Goodness-of-Fit test in this situation, if the p-Value is greater than 0.05, we will accept the null hypothesis that the data is normally distributed. That number then lets us calculate a p-Value. Using the actual number of samples in each bin and the expected number of samples, we can calculate what is called the Chi-Square Statistic in Excel. Understand the Chi-Squared Goodness-of-Fit test premise.īasically, the Chi-Squared Goodness-of-Fit test takes the number of samples in each bin on the histogram and compares that to the number of samples you might expect to find in each bin given a normal curve. If we reject the null, we accept the alternative. In statistical terms, we talk in terms of accepting or rejecting the null hypothesis.

Alternative hypothesis (Ha): The data is not normal.

Null hypothesis (Ho): The data is normal.

The two hypotheses for the Chi-Squared Goodness-of-Fit test are: That means you are testing the data with regard to a null hypothesis and an alternative hypothesis. The Chi-Squared Goodness-of-Fit test is actually a hypothesis test. If you don’t remember what the sample size was, you can refer to the count listed in the descriptive statistics.

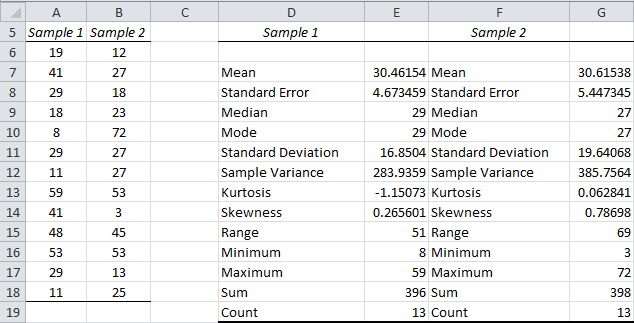
The sample size is the number of items in the data set, which was 50 for this example. The information provided are slightly similar to information in Minitab Graphical Summaryįor the Chi-Squared Goodness-of-Fit test, you will need to note the sample size (or count), the same standard deviation, and the sample mean.

Excel returns descriptive summary statistics for your data set in Sheet 3.

If you check these extra boxes, Excel will simply provide you with additional information that we won’t be using at this time. You can also check the Confidence level for mean and the Kth largest and smallest boxes, though that information isn’t required in the Chi-Squared Goodness-of-Fit test, which is the test we are running to test for normality of the data.

Ensure at least the Summary statistics box is checked.

Select to output information in a new worksheet.

In most statistical analysis, that will be the case, but if you have data grouped by rows, you should change the Grouped By selection.

In this case, the data is grouped by columns.

Click in the Input Range box and select your input range using the mouse.

Select Data > Data Analysis > Descriptive Statistics.

Use the Descriptive Statistics option in the Analysis ToolPak to quickly generate descriptive statistics for your data set in Sheet 1.

Creating a histogram using the Analysis ToolPak generates a chart and a data table, as seen below to get the ‘Frequency’ of the ‘Bin’ (Bin size is determined by the analyst).

In this post, we will share on normality test using Microsoft Excel.įor the example of the normality test, we’ll use set of data below.

#Descriptive analysis in excel for mac software

Most us are relying to our advance statistical software such as Minitab, SigmaXL, JMP and many more to validate the data normality. However, deeper analysis is require to validate the normality of the data since it is affecting our analysis method.

#Descriptive analysis in excel for mac how to

In our previous post, we have discussed what is normal distribution and how to visually identify the normal distribution.